Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Satisfiability Modulo Theories11 мая 2011Оглавление: 1. Satisfiability Modulo Theories 2. Выразительная сила SMT В программировании, Satisfiability Modulo Theories — это задача разрешимости для логических формул с учетом лежащих в их основе теорий. Примерами таких теорий для SMT формул являются: теории целых и вещественных чисел, теории списков, массивов, битовых векторов и т.д. Основные понятияФормально SMT формула — это формула в логике первого порядка, в которой некоторые функции и предикатные символы имеют дополнительную интерпретацию и задача состоит в том, чтобы определить выполнима ли данная формула. Другими словами в отличие от задачи выполнимости вместо булевых переменных SMT формула содержит произвольные переменные, а предикаты это булевы функции от этих переменных. Примерами предикатов являются линейные сравнения или равенства, включающие так называемые неинтерпретируемые термы или функциональные символы,v) = f), где f это некоторая неопределенная функция от двух аргументов). Предикаты интерпретируются согласно теории, которой они принадлежат. Например, линейные неравенства над вещественными переменными вычисляются согласно правилам теории линейной вещественной арифметики, тогда как предикаты над неинтерпретируемыми термами и функциональными символами вычисляются по правилам теории неинтерпретируемых функций с равенством. SMT включает также теории массивов и списков и теорию битовых векторов. Возможны и подтеории: например difference logic — подтеория линейной арифметики, в которой неравенства ограничены следующим видом Большинство SMT решателей поддерживают только бескванторные формулы. Просмотров: 1783
|
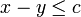 для переменных x и y и константы c.
для переменных x и y и константы c.