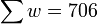Интернет магазин китайских планшетных компьютеров

Компьютеры - Ранцевая криптосистема Меркля-Хеллмана - Пример

w = {2, 7, 11, 21, 42, 89, 180, 354} - супервозрастающая последовательность.

Она является основой для генерации закрытого ключа. Посчитаем сумму элементов последовательности

Далее выберем простое число q, превосходящее полученное нами значение суммы.

q = 881

Выберем также число r из интервала [1,q)

r = 588

w, q и r образуют закрытый ключ.

Чтобы сгенерировать открытый ключ, построим последовательность β, умножая каждый элемент из последовательности w на r по модулю q.

2 * 588 mod 881 = 295
7 * 588 mod 881 = 592
11 * 588 mod 881 = 301
21 * 588 mod 881 = 14
42 * 588 mod 881 = 28
89 * 588 mod 881 = 353
180 * 588 mod 881 = 120
354 * 588 mod 881 = 236

Получим  β =.

Последовательность β образует открытый ключ.

Пусть Алиса хочет зашифровать "a". Сначала она должна перевести "a" в двоичный код

01100001

Далее она умножает каждый бит на соответствующее число из последовательности β, а сумму значений отправляет получателю.

a = 01100001
0 * 295
+ 1 * 592
+ 1 * 301
+ 0 * 14
+ 0 * 28
+ 0 * 353
+ 0 * 120
+ 1 * 236
= 1129

Чтобы расшифровать сообщение, Боб умножает полученное им значение на мультипликативное обратное r по модулю q.

1129 * 442 mod 881 = 372

После этого Боб раскладывает 372 следующим образом. Сначала он выбирает наибольший элемент из w, который меньше, чем 372, и вычисляет их разность. Далее он выбирает следующий наибольший элемент, который меньше, чем полученная разность, и повторяет эти действия, пока разность не станет равной нулю.

372 - 354 = 18
18 - 11 = 7
7 - 7 = 0

Элементы, которые были выбраны из w , будут соответствовать 1 в двоичной записи исходного текста.

01100001

Переводя обратно из двоичной записи, Боб получает, наконец, искомое "a".