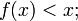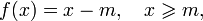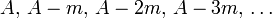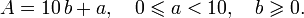Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Признаки делимости - Общие принципы построения23 января 2011Оглавление: 1. Признаки делимости 2. Общие принципы построения 3. Признаки делимости в десятичной системе счисления 4. Признаки делимости в других системах счисления Пусть требуется определить делится ли некоторое натуральное число A на другое натуральное число m. Для этого будем строить последовательность натуральных чисел: такую, что:
Тогда если последний член этой последовательности равен нулю, то A делится на m, в противном случае A на m не делится. Способ построения такой последовательности и будет искомым признаком делимости на m. Математически он может быть описан с помощью функции удовлетворяющей следующим условиям:
Если требование равноделимости для всех членов последовательности заменить на более строгое требование равноостаточности, то последний член этой последовательности будет являться остатком от деления A на m, а способ построения такой последовательности будет признаком равноостаточности на m. В силу того, что из равенства остатка при делении на m нулю следует делимость на m, любой признак равноостаточности может применяться как признак делимости. Математически признак равноостаточности тоже может быть описан с помощью функции удовлетворяющей следующим условиям:
Примером такой функции, определяющей признак равноостаточности, может быть функция а последовательность, построенная с её помощью будет иметь вид: По сути применение признака равноостаточности на базе этой функции эквивалентно делению при помощи вычитания. Другим примером может служить общеизвестный признак делимости на 10.
Математически этот признак равноостаточности может быть сформулирован следующим образом. Пусть надо выяснить остаток от деления на 10 натурального числа A, представленного в виде Тогда остатком от деления A на 10 будет a. Функция, описывающая это признак равноостаточности будет выглядеть как Легко доказать, что эта функция удовлетворяет всем перечисленным выше требованиям. Причём последовательность, построенная с её помощью, будет содержать всего один или два члена. Также легко видеть, что такой признак ориентирован именно на десятичное представление числа A — так, например, если применять его на компьютере, использующем двоичную запись числа, то чтобы выяснить a, программе пришлось бы сначала поделить A на 10. Просмотров: 7305
|
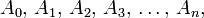
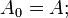
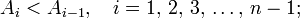
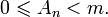
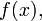 определяющей каждый следующий член последовательности в зависимости от предыдущего:
определяющей каждый следующий член последовательности в зависимости от предыдущего: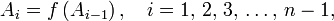
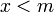 значение
значение 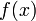 не определено;
не определено;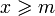 значение
значение 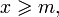 то
то