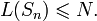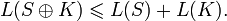|
|
|
Компьютеры - Поточный шифр - Поточные шифры на регистрах сдвига с линейной обратной связью22 января 2011
Оглавление:
1. Поточный шифр
2. Режим гаммирования для поточных шифров
3. Классификация поточных шифров
4. Поточные шифры на регистрах сдвига с линейной обратной связью
5. Потоковые шифры основанные на РСЛОС. Усложнение
6. Основные отличия поточных шифров от блочных
7. Проектирование поточных шифров
8. Криптоанализ. Атаки на поточные шифры
Теоретическая основа
Есть несколько причин использования линейных регистров сдвига в криптографии:
- высокое быстродействие криптографических алгоритмов
- применение только простейших операций сложения и умножения, аппаратно реализованных практически во всех вычислительных устройствах
- хорошие криптографические свойства
- легкость анализа с использованием алгебраических методов за счет линейной структуры
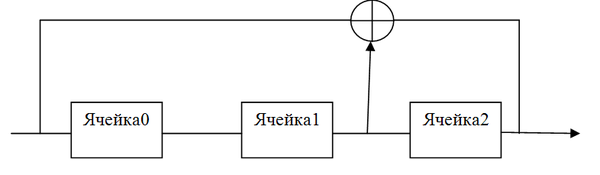
Определение: Регистр сдвига с линейной обратной связью длины L состоит из L ячеек пронумерованных 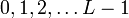 ,каждая из которых способна хранить 1 бит и имеет один вход и один выход; и синхросигнала, который контролирует смещение данных. В течение каждой единицы времени выполняются следующие операции: ,каждая из которых способна хранить 1 бит и имеет один вход и один выход; и синхросигнала, который контролирует смещение данных. В течение каждой единицы времени выполняются следующие операции:
- содержимое ячейки
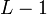 формирует часть выходной последовательности; формирует часть выходной последовательности;
- содержимое
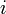 -той ячейки перемещается в ячейку -той ячейки перемещается в ячейку 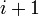 для любого для любого 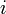 , , 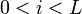 . .
- новое содержимое ячейки
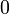 определяется битом обратной связи, который вычисляется сложением по модулю 2 с определёнными коэффициентами битов ячеек определяется битом обратной связи, который вычисляется сложением по модулю 2 с определёнными коэффициентами битов ячеек 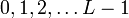 . .
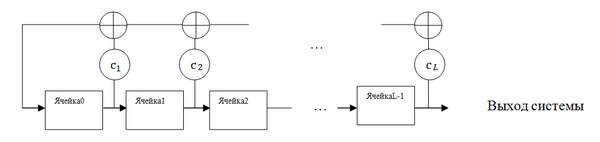
Регистр сдвига с линейной обратной связью.
На первом шаге: 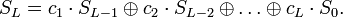
На втором шаге: 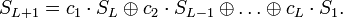
Следующее соотношение описывает в общем виде работу РСЛОС:
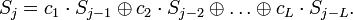
Если мы запишем во все ячейки биты равны нулю, то система будет генерировать последовательность, состоящую из всех нулей. Если записать ненулевые биты, то получим полубесконечную последовательность. Последовательность определяется коэффициентами 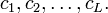
Посмотрим, каким может быть период 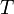 такой системы: такой системы:
Число ненулевых заполнений: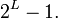 Значит, Значит, 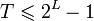 . .
После возникновения одного заполнения, которое было раньше, процесс начнёт повторяться. Процесс заполнения регистра, как показано выше, представим линейным разностным уравнением. Перенесём все члены в одну часть равенства, получим:
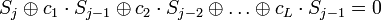 . .
Обозначим: 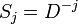 . Тогда: . Тогда:
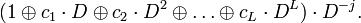
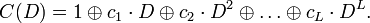
Важным свойством этого многочлена является - приводимость.
Определение:
Многочлен называется приводимым, если он может быть представлен как произведение двух многочленов меньших степеней с коэффициентами из данного поля. Если такое представление не имеет место, то многочлен называется неприводимым.
Если многочлен 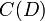 является неприводимым и примитивным, то период будет совпадать с максимально возможным периодом, равным является неприводимым и примитивным, то период будет совпадать с максимально возможным периодом, равным 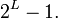
Пример.
Пример: Возьмём неприводимый примитивный многочлен 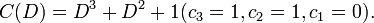 Этот многочлен можно записать, как Этот многочлен можно записать, как 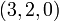 – выписаны степени, при которых стоят ненулевые коэффициенты. – выписаны степени, при которых стоят ненулевые коэффициенты.
Запишем в исходном состоянии в ячейки 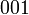 и определим длину периода генератора: и определим длину периода генератора:
Таблица. Определение периода генератора
| Обратная связь |
Ячейка0 |
Ячейка1 |
Ячейка2 |
| 1 |
0 |
0 |
1 |
| 0 |
1 |
0 |
0 |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
1 |
| 1 |
1 |
1 |
0 |
| 0 |
1 |
1 |
1 |
| 0 |
0 |
1 |
1 |
| 1 |
0 |
0 |
1 |
Период генератора равен 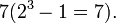 На выходе генератора буде последовательность: На выходе генератора буде последовательность: 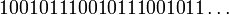
Приведём примеры некоторых примитивных многочленов по модулю 2:
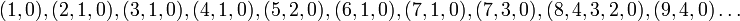
Линейная сложность
Линейная сложность бинарной последовательности – одна из самых важных характеристик работы РСЛОС. Поэтому остановимся на этой теме поподробнее.
Прежде чем дать определение линейной сложности введём некоторые обозначения.
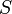 - бесконечная последовательность с членами - бесконечная последовательность с членами 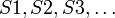
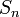 – конечная последовательность длины – конечная последовательность длины 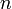 , членами которой являются , членами которой являются 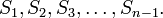
Говорят, что РСЛОС генерирует последовательность 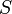 , если существует некоторое исходное состояние, при котором выходная последовательность РСЛОС совпадает с , если существует некоторое исходное состояние, при котором выходная последовательность РСЛОС совпадает с 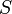 . Аналогично, говорят, что РСЛОС генерирует конечную последовательность . Аналогично, говорят, что РСЛОС генерирует конечную последовательность 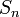 , если существует некоторое начальное состояние, для которого выходная последовательность РСЛОС имеет в качестве первых n членов члены последовательности , если существует некоторое начальное состояние, для которого выходная последовательность РСЛОС имеет в качестве первых n членов члены последовательности 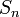 . .
Наконец дадим определение линейной сложности бесконечной двоичной последовательности.
Определение: Линейной сложностью бесконечной двоичной последовательности 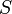 называется число называется число 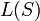 , которое определяется следующим образом: , которое определяется следующим образом:
- Если
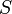 – нулевая последовательность – нулевая последовательность 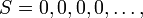 , то , то 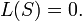
- Если не существует РСЛОС, который генерирует
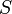 , то , то 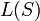 равно бесконечности. равно бесконечности.
- Иначе,
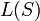 есть длина самого короткого РСЛОС, который генерирует есть длина самого короткого РСЛОС, который генерирует 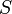 . .
Определение:
Линейной сложностью конечной двоичной последовательности 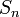 называется число называется число 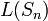 , которое равно длине самого короткого РСЛОС, который генерирует последовательность, имеющую в качестве первых , которое равно длине самого короткого РСЛОС, который генерирует последовательность, имеющую в качестве первых 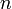 членов членов 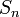 . .
Свойства линейной сложности: Пусть 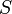 и и 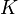 – двоичные последовательности. Тогда: – двоичные последовательности. Тогда:
1. Для любого 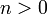 линейная сложность подпоследовательности линейная сложность подпоследовательности 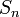 удовлетворяет неравенствам удовлетворяет неравенствам 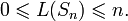
2. 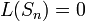 тогда и только тогда, когда тогда и только тогда, когда 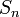 – нулевая последовательность длины – нулевая последовательность длины 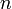 . .
3. 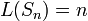 тогда и только тогда, когда тогда и только тогда, когда 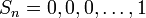 . .
4. Если 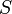 – периодическая с периодом – периодическая с периодом 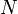 , тогда , тогда 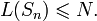
5. 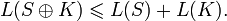
Эффективным алгоритмом определения линейной сложности конечной двоичной последовательности является алгоритм Берлекемпа-Месси.
Просмотров: 14591
|


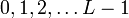 ,каждая из которых способна хранить 1 бит и имеет один вход и один выход; и синхросигнала, который контролирует смещение данных. В течение каждой единицы времени выполняются следующие операции:
,каждая из которых способна хранить 1 бит и имеет один вход и один выход; и синхросигнала, который контролирует смещение данных. В течение каждой единицы времени выполняются следующие операции: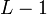 формирует часть выходной последовательности;
формирует часть выходной последовательности;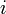 -той ячейки перемещается в ячейку
-той ячейки перемещается в ячейку 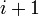 для любого
для любого 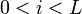 .
.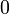 определяется битом обратной связи, который вычисляется сложением по модулю 2 с определёнными коэффициентами битов ячеек
определяется битом обратной связи, который вычисляется сложением по модулю 2 с определёнными коэффициентами битов ячеек 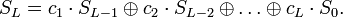
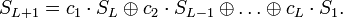
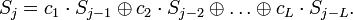
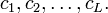
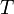 такой системы:
такой системы: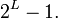 Значит,
Значит, 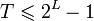 .
.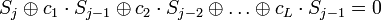 .
.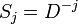 . Тогда:
. Тогда: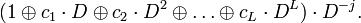
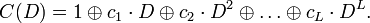
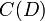 является неприводимым и примитивным, то период будет совпадать с максимально возможным периодом, равным
является неприводимым и примитивным, то период будет совпадать с максимально возможным периодом, равным 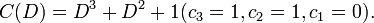 Этот многочлен можно записать, как
Этот многочлен можно записать, как 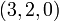 – выписаны степени, при которых стоят ненулевые коэффициенты.
– выписаны степени, при которых стоят ненулевые коэффициенты.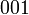 и определим длину периода генератора:
и определим длину периода генератора: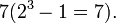 На выходе генератора буде последовательность:
На выходе генератора буде последовательность: 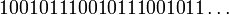
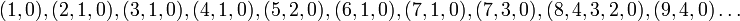
 - бесконечная последовательность с членами
- бесконечная последовательность с членами 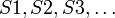
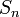 – конечная последовательность длины
– конечная последовательность длины 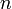 , членами которой являются
, членами которой являются 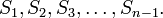
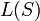 , которое определяется следующим образом:
, которое определяется следующим образом: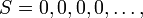 , то
, то 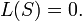
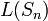 , которое равно длине самого короткого РСЛОС, который генерирует последовательность, имеющую в качестве первых
, которое равно длине самого короткого РСЛОС, который генерирует последовательность, имеющую в качестве первых 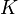 – двоичные последовательности. Тогда:
– двоичные последовательности. Тогда: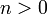 линейная сложность подпоследовательности
линейная сложность подпоследовательности 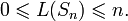
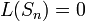 тогда и только тогда, когда
тогда и только тогда, когда 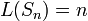 тогда и только тогда, когда
тогда и только тогда, когда 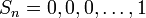 .
.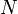 , тогда
, тогда