Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Оптический поток23 января 2011Оглавление: 1. Оптический поток 2. Использование оптического потока это изображение видимого движения объектов, поверхностей или краев сцены, получаемое в результате перемещения наблюдателя относительно сцены. Алгоритмы, основанные на оптическом потоке, такие как регистрация движения, сегментация объектов, кодирование движений и подсчет диспаритета в стерео используют это движение объектов, поверхностей и краев. Оценка оптического потокаПоследовательности упорядоченных изображений позволяют оценивать движение либо как мгновенную скорость изображения, либо как дискретное смещение. Fleet и Weiss составили учебный курс по градиентному методу оценки оптического потока. Анализ методов вычисления оптического потока проведен в работе John L. Barron, David J. Fleet и Steven Beauchemin. Они раccматривают методы как с точки зрения точности, так и с точки зрения плотности получаемого векторного поля. Методы, основанные на оптическом потоке, вычисляют движение между двумя кадрами, взятыми в момент времени В случае размерности 2D+t пиксель в позиции с интенсивностью Считая, что перемещение мало, и используя ряд Тейлора, получаем:
Из этих равенств следует: или отсюда получается, что где или Полученное уравнение содержит две неизвестных и не может быть однозначно разрешено. Данное обстоятельство известно как проблема апертуры. Задачу решает наложение дополнительных ограничений - регуляризация. Методы определения оптического потока
Просмотров: 2722
|
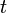 и
и 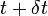 , в каждом пикселе. Эти методы называются дифференциальными, так как они основаны на приближении сигнала отрезком ряда Тейлора; таким образом, они используют частные производные по времени и пространственным координатам.
, в каждом пикселе. Эти методы называются дифференциальными, так как они основаны на приближении сигнала отрезком ряда Тейлора; таким образом, они используют частные производные по времени и пространственным координатам.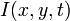 за один кадр будет перемещен на
за один кадр будет перемещен на 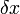 ,
, 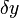 и
и 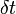 , и можно записать следующее уравнение:
, и можно записать следующее уравнение: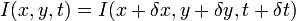
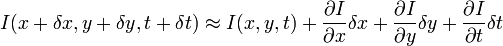 .
.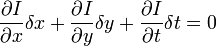
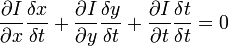
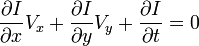
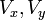 это
это 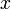 и
и 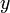 компоненты скорости оптического потока в
компоненты скорости оптического потока в 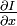 ,
, 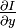 и
и 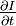 это производные изображения в
это производные изображения в 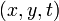 в соответствующих направлениях. Таким образом:
в соответствующих направлениях. Таким образом: