Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Односторонняя функция - Односторонние функции в криптографических схемах22 января 2011Оглавление: 1. Односторонняя функция 2. Определение 3. Односторонние функции в криптографических схемах 4. Кандидаты в односторонние функции Существование односторонних функций является необходимым условием для стойкости многих типов криптографических схем. В некоторых случаях этот факт устанавливается достаточно просто. Рассмотрим функцию f такую, что f = K1. Она вычислима с помощью алгоритма G за полиномиальное время. Покажем, что если f не односторонняя функция, то криптосистема нестойкая. Предположим, что существует полиномиальный вероятностный алгоритм A, который инвертирует f с вероятностью по крайней мере 1/p для некоторого полинома p. Здесь n - длина ключа K1. Атакующий может подать на вход алгоритму A ключ K1 и получить с указанной вероятностью некоторое значение r' из прообраза. Далее злоумышленник подает r' на вход алгоритма G и получает пару ключей . Хотя K'2 не обязательно совпадает с K2, тем не менее, по определению криптосистемы Из всего сказанного следует, что предположение о существовании односторонних функций является самым слабым криптографическим предположением, которое может оказаться достаточным для доказательства существования стойких криптографических схем различных типов. На выяснение того, является ли это условие и в самом деле достаточным, направлены значительные усилия специалистов. Трудность задачи построения криптографических схем из односторонних функций можно пояснить на следующем примере. Пусть f - односторонняя функция и нам требуется построить криптосистему с секретным ключом. В такой криптосистеме имеется только один ключ - секретный, который известен и отправителю, и получателю шифрованного сообщения. Алгоритмы шифрования EK и дешифрования DK оба зависят от этого секретного ключа K и таковы, что DK) = m для любого открытого текста m. Ясно, что если криптограмму d сообщения m вычислять как d = f, то противник, перехвативший d, может вычислить m лишь с пренебрежимо малой вероятностью. Но во-первых, непонятно, каким образом сможет восстановить сообщение m из криптограммы законный получатель? Во-вторых, из того, что функция f односторонняя следует лишь, что противник не может вычислить все сообщение целиком. А это - весьма низкий уровень стойкости. Желательно, чтобы противник, знающий криптограмму d, не мог вычислить ни одного бита открытого текста. На настоящий момент доказано, что существование односторонних функций является необходимым и достаточным условием для существования стойких криптосистем с секретным ключом, а также стойких криптографических протоколов нескольких типов, включая протоколы электронной подписи. Просмотров: 4142
|
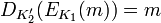 для любого открытого текста m. Поскольку K'2 найден с вероятностью по крайней мере 1/p, которая в криптографии не считается пренебрежимо малой, криптосистема нестойкая.
для любого открытого текста m. Поскольку K'2 найден с вероятностью по крайней мере 1/p, которая в криптографии не считается пренебрежимо малой, криптосистема нестойкая.