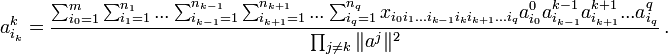Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Метод главных компонент - Сингулярное разложение матрицы данных22 января 2011Оглавление: 1. Метод главных компонент 2. Формальная постановка задачи 3. Диагонализация ковариационной матрицы 4. Сингулярное разложение матрицы данных 5. Матрица преобразования к главным компонентам 6. Отбор главных компонент по правилу Кайзера 7. Оценка числа главных компонент по правилу сломанной трости 8. Нормировка 9. Механическая аналогия и метод главных компонент для взвешенных данных 10. Специальная терминология 11. Примеры использования Идея сингулярного разложенияМатематическое содержание метода главных компонент — это спектральное разложение ковариационной матрицы C, то есть представление пространства данных в виде суммы взаимно ортогональных собственных подпространств C, а самой матрицы C — в виде линейной комбинации ортогональных проекторов на эти подпространства с коэффициентами λi. Если Число Пусть где σl > 0 — сингулярное число, Хотя формально задачи сингулярного разложения матрицы данных и спектрального разложения ковариационной матрицы совпадают, алгоритмы вычисления сингулярного разложения напрямую, без вычисления ковариационной матрицы и её спектра, более эффективны и устойчивы . Теория сингулярного разложения была создана Дж. Дж. Сильвестром в 1889 г. и изложена во всех подробных руководствах по теории матриц . Простой итерационный алгоритм сингулярного разложенияОсновная процедура — поиск наилучшего приближения произвольной Решение этой задачи дается последовательными итерациями по явным формулам. При фиксированном векторе a = значения b =, доставляющие минимум форме F, однозначно и явно определяются из равенств Аналогично, при фиксированном векторе b = определяются значения a =: B качестве начального приближения вектора a возьмем случайный вектор единичной длины, вычисляем вектор b, далее для этого вектора b вычисляем вектор a и т. д. Каждый шаг уменьшает значение F. В качестве критерия остановки используется малость относительного уменьшения значения минимизируемого функционала F за шаг итерации или малость самого значения F. В результате для матрицы X = получили наилучшее приближение матрицей P1 вида К достоинствам этого алгоритма относится его исключительная простота и возможность почти без изменений перенести его на данные с пробелами, а также взвешенные данные. Существуют различные модификации базового алгоритма, улучшающие точность и устойчивость. Например, векторы главных компонент a при разных l должны быть ортогональны «по построению», однако при большом числе итерации малые отклонения от ортогональности накапливаются и может потребоваться специальная коррекция a на каждом шаге, обеспечивающая его ортогональность ранее найденным главным компонентам. Для квадратных симметричных положительно определённых матриц описанный алгоритм превращается в метод прямых итераций для поиска собственных векторов. Сингулярное разложение тензоров и тензорный метод главных компонентЧасто вектор данных имеет дополнительную структуру прямоугольной таблицы или даже многомерной таблицы — то есть тензора: Основная процедура — поиск наилучшего приближения тензора Решение этой задачи дается последовательными итерациями по явным формулам. Если заданы все векторы-сомножители кроме одного B качестве начального приближения векторов Это многокомпонентное сингулярное разложение успешно применяется при обработке изображений, видеосигналов, и, шире, любых данных, имеющих табличную или тензорную структуру. Просмотров: 23145
|
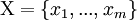 — матрица, составленная из векторов-столбцов центрированных данных, то
— матрица, составленная из векторов-столбцов центрированных данных, то 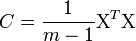 и задача о спектральном разложении ковариационной матрицы C превращается в задачу о сингулярном разложении матрицы данных
и задача о спектральном разложении ковариационной матрицы C превращается в задачу о сингулярном разложении матрицы данных 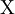 .
.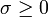 называется сингулярным числом матрицы
называется сингулярным числом матрицы 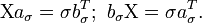
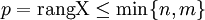 — ранг матрицы данных. Сингулярное разложение матрицы данных
— ранг матрицы данных. Сингулярное разложение матрицы данных 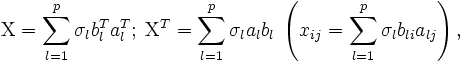
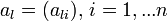 — соответствующий правый сингулярный вектор-столбец, а
— соответствующий правый сингулярный вектор-столбец, а 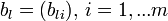 — соответствующий левый сингулярный вектор-строка. Правые сингулярные векторы-столбцы al, участвующие в этом разложении, являются векторами главных компонент и собственными векторами эмпирической ковариационной матрицы
— соответствующий левый сингулярный вектор-строка. Правые сингулярные векторы-столбцы al, участвующие в этом разложении, являются векторами главных компонент и собственными векторами эмпирической ковариационной матрицы 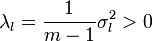 .
. матрицы X = матрицей вида
матрицы X = матрицей вида 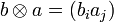 методом наименьших квадратов:
методом наименьших квадратов: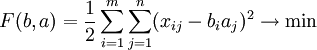
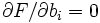 :
: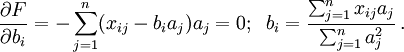
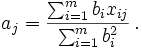
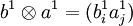 . Далее, из матрицы X вычитаем полученную матрицу P1, и для полученной матрицы уклонений X1 = X − P1 вновь ищем наилучшее приближение P2 этого же вида и т. д., пока, например, норма Xk не станет достаточно малой. В результате получили итерационную процедуру разложения матрицы X в виде суммы матриц ранга 1, то есть
. Далее, из матрицы X вычитаем полученную матрицу P1, и для полученной матрицы уклонений X1 = X − P1 вновь ищем наилучшее приближение P2 этого же вида и т. д., пока, например, норма Xk не станет достаточно малой. В результате получили итерационную процедуру разложения матрицы X в виде суммы матриц ранга 1, то есть 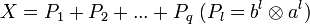 . Полагаем
. Полагаем 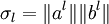 и нормируем векторы
и нормируем векторы 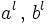 :
: 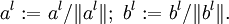 В результате получена аппроксимация сингулярных чисел σl и сингулярных векторов.
В результате получена аппроксимация сингулярных чисел σl и сингулярных векторов.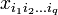 ,
, 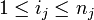 . В этом случае также эффективно применять сингулярное разложение. Определение, основные формулы и алгоритмы переносятся практически без изменений: вместо матрицы данных имеем q + 1-индексную величину
. В этом случае также эффективно применять сингулярное разложение. Определение, основные формулы и алгоритмы переносятся практически без изменений: вместо матрицы данных имеем q + 1-индексную величину 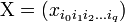 , где первый индекс i0-номер точки данных.
, где первый индекс i0-номер точки данных.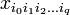 тензором вида
тензором вида 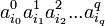 " src="http://upload.wikimedia.org/math/0/d/d/0dd71a561a8ee7d34bca45721a95490e.png" /> — m-мерный вектор,
" src="http://upload.wikimedia.org/math/0/d/d/0dd71a561a8ee7d34bca45721a95490e.png" /> — m-мерный вектор, 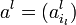 — вектор размерности nl при l > 0) методом наименьших квадратов:
— вектор размерности nl при l > 0) методом наименьших квадратов: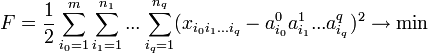
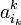 , то этот оставшийся определяется явно из достаточных условий минимума.
, то этот оставшийся определяется явно из достаточных условий минимума.