|
|
|
23 января 2011
Оглавление:
1. Метод эллипсоидов
2. Применение к задаче линейного программирования
Описание алгоритма
В начале выбирается большой шар, содержащий пересечение выпуклых множеств. Способ построения этого шара зависит от задачи. Далее на каждом шаге имеется эллипсоид, заданный центром v и векторами 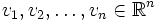 . Эллипсоиду принадлежат точки . Эллипсоиду принадлежат точки 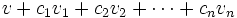 для которых для которых  . Отметим, что один и тот же эллипсоид можно задать несколькими способами. Если центр этого эллипсоида принадлежит всем выпуклым множествам, то искомая точка найдена. Иначе существует гиперплоскость π, проходящая через точку v, такая, что одно из множеств целиком лежит по одну сторону от нее. Тогда можно перейти от исходного базиса vi к другому базису . Отметим, что один и тот же эллипсоид можно задать несколькими способами. Если центр этого эллипсоида принадлежит всем выпуклым множествам, то искомая точка найдена. Иначе существует гиперплоскость π, проходящая через точку v, такая, что одно из множеств целиком лежит по одну сторону от нее. Тогда можно перейти от исходного базиса vi к другому базису 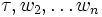 такому, что wi параллельны π, а τ направлен в сторону множества. Положим теперь такому, что wi параллельны π, а τ направлен в сторону множества. Положим теперь 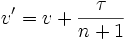 , , 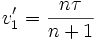 , , 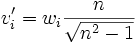 при при 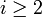 . Этот новый эллипсоид содержит половину старого и имеет меньший объем. Таким образом, объем эллипсоида уменьшается экспоненциально с ростом числа шагов и искомая точка будет найдена за O) шагов, где V1 — объем исходного шара, а V2 — объем области пересечения. Общее время работы алгоритма получается равным O), где N — число множеств, t — время проверки принадлежности точки множеству. . Этот новый эллипсоид содержит половину старого и имеет меньший объем. Таким образом, объем эллипсоида уменьшается экспоненциально с ростом числа шагов и искомая точка будет найдена за O) шагов, где V1 — объем исходного шара, а V2 — объем области пересечения. Общее время работы алгоритма получается равным O), где N — число множеств, t — время проверки принадлежности точки множеству.
Просмотров: 2747
|
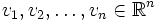 . Эллипсоиду принадлежат точки
. Эллипсоиду принадлежат точки 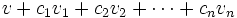 для которых
для которых  . Отметим, что один и тот же эллипсоид можно задать несколькими способами. Если центр этого эллипсоида принадлежит всем выпуклым множествам, то искомая точка найдена. Иначе существует гиперплоскость π, проходящая через точку v, такая, что одно из множеств целиком лежит по одну сторону от нее. Тогда можно перейти от исходного базиса vi к другому базису
. Отметим, что один и тот же эллипсоид можно задать несколькими способами. Если центр этого эллипсоида принадлежит всем выпуклым множествам, то искомая точка найдена. Иначе существует гиперплоскость π, проходящая через точку v, такая, что одно из множеств целиком лежит по одну сторону от нее. Тогда можно перейти от исходного базиса vi к другому базису 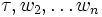 такому, что wi параллельны π, а τ направлен в сторону множества. Положим теперь
такому, что wi параллельны π, а τ направлен в сторону множества. Положим теперь 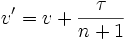 ,
, 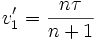 ,
, 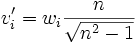 при
при 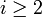 . Этот новый эллипсоид содержит половину старого и имеет меньший объем. Таким образом, объем эллипсоида уменьшается экспоненциально с ростом числа шагов и искомая точка будет найдена за O) шагов, где V1 — объем исходного шара, а V2 — объем области пересечения. Общее время работы алгоритма получается равным O), где N — число множеств, t — время проверки принадлежности точки множеству.
. Этот новый эллипсоид содержит половину старого и имеет меньший объем. Таким образом, объем эллипсоида уменьшается экспоненциально с ростом числа шагов и искомая точка будет найдена за O) шагов, где V1 — объем исходного шара, а V2 — объем области пересечения. Общее время работы алгоритма получается равным O), где N — число множеств, t — время проверки принадлежности точки множеству.