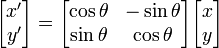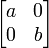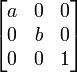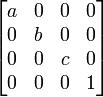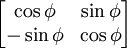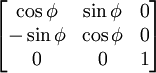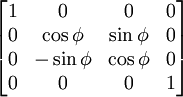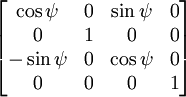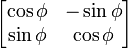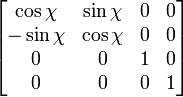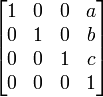|
|
|
23 января 2011
Оглавление:
1. Матрица перехода
2. Свойства
Матрицей перехода от базиса 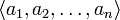 к базису к базису 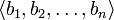 является матрица, столбцы которой — координаты разложения векторов является матрица, столбцы которой — координаты разложения векторов 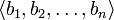 в базисе в базисе 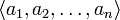 . .
Обозначается 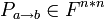
Использование
При умножении столбца, составленного из коэффициентов разложения вектора по базису 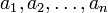 , на матрицу, обратную к матрице перехода, мы получаем тот же вектор, выраженный через базис , на матрицу, обратную к матрице перехода, мы получаем тот же вектор, выраженный через базис 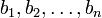 . .
Из-за того, что уменьшает объём работы при переводе векторов аффинных пространств и в пространстве столбцов Rв другие базисы, используется в трёхмерном моделировании.
Пример
Для того, чтобы повернуть вектор на угол θ против часовой стрелки, можно умножить матрицу поворота на него:
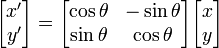
| Матрицы наиболее распространённых преобразований |
|
В двумерных координатах |
В однородных двумерных координатах |
В однородных трёхмерных координатах |
| Масштабирование
При a, b и c - коэффициенты масштабирования соответственно по осям OX, OY и OZ:
|
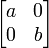
|
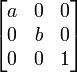
|
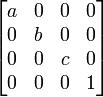
|
| Поворот
При φ - угол поворота изображения в двухмерном пространстве
|
По часовой стрелке
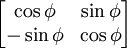
|
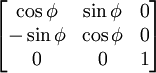
|
Относительно OX на угол φ
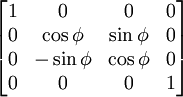
|
Относительно OY на угол ψ
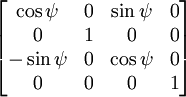
|
|
Против часовой стрелки
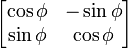
|
Относительно OZ на угол χ
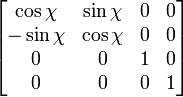
|
| Перемещение
При a, b и c - смещение соответственно по осям OX, OY и OZ.
|
В неоднородных координатах не имеет матричного представления.
|

|
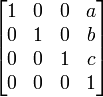
|
Просмотров: 7596
|
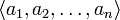 к базису
к базису 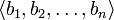 является матрица, столбцы которой — координаты разложения векторов
является матрица, столбцы которой — координаты разложения векторов 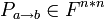
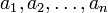 , на матрицу, обратную к матрице перехода, мы получаем тот же вектор, выраженный через базис
, на матрицу, обратную к матрице перехода, мы получаем тот же вектор, выраженный через базис 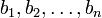 .
.