Интернет магазин китайских планшетных компьютеров

Компьютеры - Marching cubes

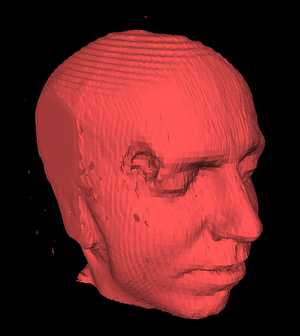
Модель, построенная из 150 слоев с МРТ с использованием алгоритма marching-cubes. Под поверхностью находятся около 150 000 полигонов и скрытых объектов. Размер сетки составляет 64 × 64 × 150 вокселей, кодированных 8-ю битами. Для сглаживания поверхности модели был применён пре-процессинг. «Дырка» в области виска является следствием пирсинга подопытного.

Marching cubes — алгоритм в компьютерной графике, впервые предложенный в 1987 году на конференции SIGGRAPH Вильямом Лоренсеном и Харви Клайном, для обработки полигональной сетки изоповерхности трехмерного скалярного поля. Аналогичный алгоритм на плоскости называется marching squares.

Принцип работы

Алгоритм пробегает скалярное поле, на каждой итерации просматривает 8 соседних позиций и определяет полигоны, необходимые для представления части изоповерхности, проходящей через данный куб. Далее на экран выводятся полигоны, образующие заданную изоповерхность.

Так как алгоритм выбирает полигоны, исходя только из положения вершин куба относительно изоповерхности, всего получается 256 возможных конфигураций полигонов, которые можно вычислить заранее и сохранить в массиве. Поэтому каждый куб можно представить восьмибитным числом, сопоставив каждой вершине 1, если значение поля в точке больше, чем на изоповерхности, и 0 в противном случае. Полученное число используется в качестве индекса элемента массива, хранящего конфигурации полигонов. Наконец каждая вершина сгенерированного полигона помещается в подходящую позицию на том ребре куба, на котором она лежала изначально. Позиция вычисляется путем линейной интерполяции значений скалярного поля в концах ребра.

15 различных конфигураций куба

Заранее вычисленный массив из 256 конфигураций полигонов можно получить поворотами и отражениями 15 различных конфигураций куба. Однако использование всего 15 базовых конфигураций не гарантирует получение замкнутой поверхности. Базовые конфигурации, лишенные этого недостатка, можно найти в специальной литературе.

Градиент скалярного поля в каждой точке сетки также является нормальным вектором предполагаемой изоповерхности, проходящей через эту точку. Поэтому возможно интерполировать эти нормали вдоль ребер каждого куба, чтобы найти нормали сгенерированных вершин, для корректного отображения модели при использовании освещения.

Данный алгоритм широко используется в медицине, например, в компьютерной и магнитно-резонансной томографии, а также для 3D моделирования метасфер или других метаповерхностей.