Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Кватернионы и вращение пространства23 января 2011
Организация всех трёх степеней свободы, однако окончательная свобода наименьшего кольца зависит от положения старших колец.
Кватернионы предоставляют удобное математическое обозначение положения и вращения объектов в пространстве. В сравнении с углами Эйлера, кватернионы позволяют проще комбинировать вращения, а также избежать проблемы, связанной с невозможностью поворота вокруг оси, независимо от совершённого вращения по другим осям. В сравнении с матрицами они обладают большей вычислительной устойчивостью и могут быть более эффективными. Кватернионы нашли своё применение в компьютерной графике, робототехнике, навигации, молекулярной динамике. Операции вращенияВ этой секции даётся очень краткое описание из книги автора Altmann. Представление пространства вращенияЕдиничный кватернион представляет прямой способ вращения в математическом пространстве в трёх измерениях. Соответствие между вращениями и кватернионами в первую очередь может быть осознано через само пространство вращения. 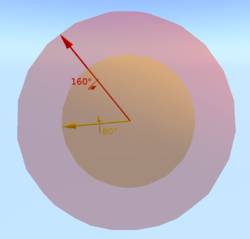
Два вращения вокруг разных осей и на разные углы в пространстве вращений.
Любое вращение в трёхмерном пространстве — это вращение на определённый угол вокруг определённой оси. Если угол равен нулю, то выбор оси не имеет значения, таким образом вращения на угол ноль градусов — это точка в пространстве вращения. Для крошечного, но ненулевого вращения, каждое возможное вращение — это маленькая сфера, окружающая единичное вращение, где каждая точка на этой сфере представляет собой ось, указывающую в определённом направлении. Чем больше угол вращения, тем дальше вращение от единичного вращения — о таких вращениях можно думать как о концентрических сферах с увеличивающимся радиусом. Таким образом, вблизи единичного вращения абстрактное пространство вращений выглядит как обычное трёхмерное пространство. При увеличении угла до 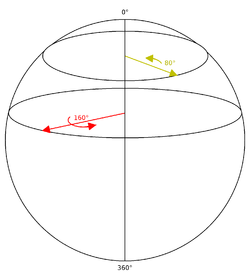
Гиперсфера вращений для вращений имеющих "горизонтальную" ось.
Мы можем увидеть похожее поведение на поверхности сферы. Если мы расположимся на северном полюсе и начнём чертить прямые линии, исходящие из него в различных направлениях, то сначала они будут расходиться, но затем снова сойдутся на южном полюсе. Концентрические круги, получившиеся вокруг северного полюса, стянутся в одну точку на южном полюсе — когда радиус сферы сравняется с расстоянием между полюсами. Если думать о разных направлениях из полюса как о разных осях вращения, а о разных расстояниях от полюса как о разных углах вращения, то мы получим пространство для вращений. Получившаяся сфера представляет вращение в трёхмерном пространстве, хотя является двухмерной поверхностью, что не позволяет смоделировать гиперсферу. Однако двухмерную поверхность сферы можно представлять как часть гиперсферы. Мы можем взять часть, например, для представления вращения вокруг осей в плоскостях x и y. Важно отметить, что угол вращения до экватора равен 180°; до южного полюса 360°. Северный и южный полюс представляют одинаковые вращения. Это справедливо для двух любых диаметрально противоположных точек: если одна точка — это вращение на угол α вокруг оси v, то диаметрально противоположной является точка с вращением на угол Определение пространства вращенияПоверхность сферы можно охарактеризовать двумя координатами, например широтой и долготой. Однако такие координаты как широта и долгота на северном и южном полюсах начинают вести себя неопределённо, хотя северный и южный полюса принципиально не отличаются от любой другой точки поверхности сферы. Это показывает, что ни одна координатная система не может двумя координатами охарактеризовать положение в пространстве. Этого можно избежать поместив сферу в трёхмерное пространство, охарактеризовав её декартовыми координатами, помещая северный полюс на =, южный полюс на =, а экватор на w = 0, x² + y² = 1. Точки на сфере удовлетворяют отношению w² + x² + y² = 1. В итоге получаются две степени свободы, хотя имеется три координаты. Точка представляет вращение вокруг осей на угол Таким же образом гиперсферическое пространство трёхмерных вращений может быть охарактеризовано тремя углами, однако любое такое представление начинает вырождаться на некоторых точках гиперсферы. Этой проблемы можно избежать, используя евклидовы координаты w, x, y, z, где w² + x² + y² + z² = 1. Точка представляет вращение вокруг осей на угол Коротко о кватернионахКомплексное число может быть определено введением абстрактного символа i, который удовлетворяет обычным правилам алгебры, а также правила i = − 1. Этого достаточно для воспроизведения всех правил арифметики комплексных чисел. Например:
Таким же образом кватернионы могут быть определены введением абстрактных символов i, j, k, умножение которых задаются по правилу а умножение на вещественные числа определяются обычным образом, причём умножение полагается ассоциативным, но не коммутативным. Из этого следуют все правила кватернионной арифметики, например
Мнимая часть
Векторное произведение некоммутативно, а произведения скаляр-скаляр и скаляр-вектор коммутативны. Из этих правил следует:
Обратным для ненулевого кватерниона
что может быть проверено прямым вычислением. Определение пространства вращения через кватернионыДопустим — координаты вращения, согласно прежнему описанию. Тогда кватернион q можно определить как
где вращает вектор Вращение на кватернионы можно объединить, перемножив их. Таким образом, вращения на кватернионы p и q равно что то же самое, что и вращение на q, а затем на p. Инверсия кватерниона — это то же, что и вращение в противоположном направлении, таким образом Вращение на единичный кватернионПусть u — это единичный вектор, а вращает вектор v на угол α вокруг оси u. Раскрыв скобки, получаем где Просмотров: 4175
|
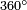 вращения вокруг различных осей перестают расходиться и начинают становиться похожими друг на друга, становясь идентичными когда угол достигает 360 градусов.
вращения вокруг различных осей перестают расходиться и начинают становиться похожими друг на друга, становясь идентичными когда угол достигает 360 градусов.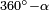 вокруг оси −v. Таким образом, пространство вращений является не самой гиперсферой, а гиперсферой радиуса π с отождествлёнными диаметрально противоположными точками. Однако для большинства целей можно думать о вращениях как о точках на сфере, несмотря на то что они обладают двойной избыточностью.
вокруг оси −v. Таким образом, пространство вращений является не самой гиперсферой, а гиперсферой радиуса π с отождествлёнными диаметрально противоположными точками. Однако для большинства целей можно думать о вращениях как о точках на сфере, несмотря на то что они обладают двойной избыточностью.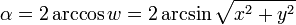 .
.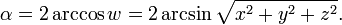
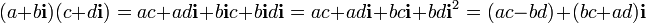 .
.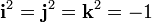
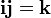
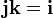
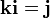
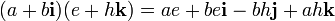 .
.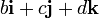 кватерниона ведёт себя так же, как и вектор
кватерниона ведёт себя так же, как и вектор 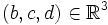 , а вещественная часть a ведёт себя так же, как и скаляр в
, а вещественная часть a ведёт себя так же, как и скаляр в  . При использовании кватернионов удобнее описывать их как скаляр и вектор и использовать векторное и скалярное произведения
. При использовании кватернионов удобнее описывать их как скаляр и вектор и использовать векторное и скалярное произведения  и
и  . При этом они связаны с обычным кватернионным умножением следующей формулой:
. При этом они связаны с обычным кватернионным умножением следующей формулой: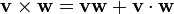 .
.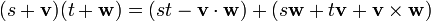 .
.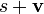 является
является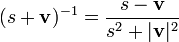 ,
,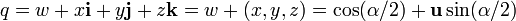 ,
,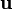 — единичный вектор. Таким образом, произведение
— единичный вектор. Таким образом, произведение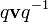
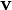 на угол α вокруг оси
на угол α вокруг оси 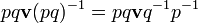
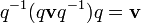 . Квадрат кватерниона — это вращение на двойной угол вокруг той же оси. В общем смысле, q — это вращение вокруг оси q на угол в n раз больший первоначального. Вместо n может быть любое вещественное число, позволяя использовать кватернионы для плавной интерполяции между двумя положениями в пространстве.
. Квадрат кватерниона — это вращение на двойной угол вокруг той же оси. В общем смысле, q — это вращение вокруг оси q на угол в n раз больший первоначального. Вместо n может быть любое вещественное число, позволяя использовать кватернионы для плавной интерполяции между двумя положениями в пространстве.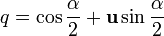 кватернион. Наша цель показать, что
кватернион. Наша цель показать, что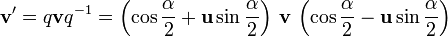
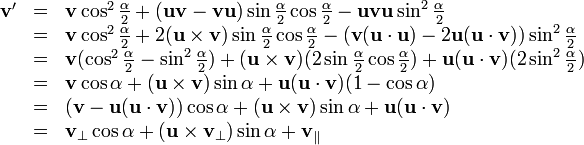
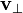 и
и 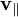 — это компоненты вектора v, которые перпендикулярны и параллельны оси u соответственно. Получившийся результат является формулой вращения на угол α вокруг оси u.
— это компоненты вектора v, которые перпендикулярны и параллельны оси u соответственно. Получившийся результат является формулой вращения на угол α вокруг оси u.