Интернет магазин китайских планшетных компьютеров |
||||
Компьютеры - Компьютер для операций с функциями - Позиционные коды функций одного аргумента23 января 2011Оглавление: 1. Компьютер для операций с функциями 2. Позиционные коды функций одного аргумента 3. Позиционные коды функций многих аргументов Основная идеяПозиционный код целого числа A представляет собой запись цифр α этого числа в некоторой позиционной системе счисления, имеющую вид Такой код можно назвать линейным. В отличие от него позиционный код функции F одного аргумента x имеет вид то есть является плоским и треугольным, поскольку цифры в нем образуют треугольник.
где ρ — основание данной системы счисления. Указанному позиционному коду функции одного аргумента соответствует двойная сумма вида
где R — целое положительное число, количество значений цифры α, y — определенная функция аргумента x.
Сложение позиционных кодов функций одного аргумента также связано с передачей переноса по схеме
При этом один и тот же перенос передается одновременно в два старших разряда. R-ые треугольные кодыТреугольный код называется R-ым, если числа αmk принимают значения из множества
Например, треугольный код является троичным TK3, если
где a — любое число. Существует TKR любого целого действительного числа. В частности, TKR = α. Также существует TKR любой функции вида y. В частности, Одноразрядное сложениев R-ых треугольных кодах состоит в том, что
Эта процедура описывается таблицей одноразрядного сложения, где должны присутствовать все значения слагаемых
Одноразрядное вычитаниев R-ых треугольных кодах отличается от одноразрядного сложения только тем, что в данном -разряде величина
Одноразрядное деление на параметр Rв R-ых треугольных кодах основано на использовании соотношения
откуда следует, что деление каждого разряда вызывает переносы в два нижних разряда. Следовательно, разрядный результат в этой операции является суммой частного от деления данного разряда на R и переносов из двух верхних разрядов. Таким образом, при делении на параметр R
Эта процедура описывается таблицей одноразрядного деления на параметр R, где должны присутствовать все значения слагаемых и все значения переносов, возникающих при разложении суммы
Сложение и вычитаниеR-ых треугольных кодов состоит в последовательно выполняемых одноразрядных операциях. При этом одноразрядные операции во всех разрядах каждого столбца выполняются одновременно. УмножениеR-ых треугольных кодов. Умножение некоторого кода TKR' на -разряд другого кода TKR'' заключается в -сдвиге кода TKR', то есть сдвиге его на k столбцов влево и на m строк вверх. Умножение кодов TKR' и TKR'' заключается в последовательных -сдвигах кода TKR' и сложениях сдвинутого кода TKR' с частичным произведением. ДифференцированиеR-ых треугольных кодов. Производная функции F, определенной выше,
Поэтому дифференцирование треугольных кодов функции F заключается в определении треугольного кода частной производной
Cпособ дифференцирования заключается в организации переносов из mk-разряда в-разряд и в-разряд, а их суммирование в данном разряде производится аналогично одноразрядному сложению. Кодирование и декодированиеR-ых треугольных кодов. Функция, представленная рядом вида
с целыми коэффициентами Ak, может быть представлена R-ым треугольным кодом, так как эти коэффициенты и функции y имеют R-ые треугольные коды. С другой стороны, R-ый треугольный код может быть представлен указанным рядом, так как любое слагаемое αmkRy в позиционном разложении функции может быть представлено таким же рядом. УкорочениеR-ых треугольных кодов. Так называется операция уменьшения числа ненулевых столбцов. Необходимость укорочения возникает при возникновении переносов за разрядную сетку. Укорочение заключается в делении на параметр R. При этом все коэффициенты представимого кодом ряда уменьшаются в R раз, а дробные части этих коэффициентов отбрасываются. Исчезает также старший член ряда. Такое сокращение допустимо, если известно, что ряды функций являются сходящимися. Укорочение состоит в последовательно выполняемых одноразрядных операциях деления на параметр R. При этом одноразрядные операции во всех разрядах каждой строки выполняются одновременно, а переносы из младшей строки отбрасываются. Масштабный коэффициентR-ый треугольный код сопровождается масштабным коэффициентом M, аналогичным порядку в числе с плавающей точкой. Коэффициент M позволяет представить все коэффиценты кодируемого ряда в виде целых чисел. Коэффициент M умножается на R при укорочении кода. При сложении коэффициенты M выравниваются, для чего необходимо укорачивать один из слагаемых кодов. При умножении коэффициенты M также умножаются. Просмотров: 3692
|
||||
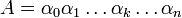
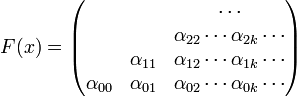
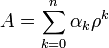 ,.
,.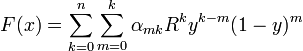 ,
,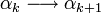 .
.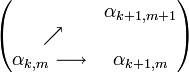 .
.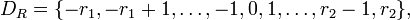 где
где 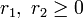 и
и 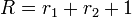 .
.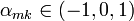 , и — четверичным TK4, если
, и — четверичным TK4, если 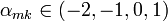 .
.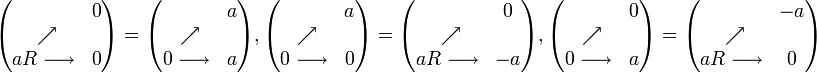 ,
,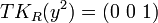 .
.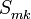 слагаемых разрядов
слагаемых разрядов 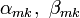 и двух переносов
и двух переносов 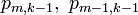 , поступивших в данный разряд слева, то есть
, поступивших в данный разряд слева, то есть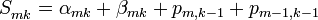 ,
,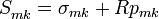 , где
, где 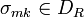 ,
,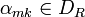 и
и 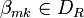 и все значения переносов, возникающих при разложении суммы
и все значения переносов, возникающих при разложении суммы 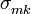
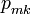
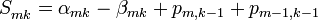 .
.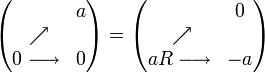 ,
,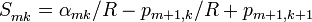 ,
,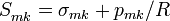 , где
, где 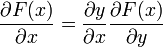 .
.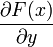 и умножении его на известный треугольный код производной
и умножении его на известный треугольный код производной 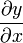 . Определение треугольного кода частной производной
. Определение треугольного кода частной производной 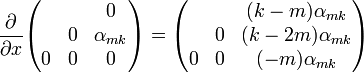 .
.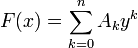 ,
,