Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Коды Голомба23 января 2011Оглавление: 1. Коды Голомба 2. Пример семейство энтропийных кодов. Под кодом Голомба может подразумеваться также один из представителей этого семейства. Рассмотрим источник, независимым образом порождающий целые неотрицательные числа i с вероятностями P =p, где p — произвольное положительное число, не превосходящее 1, т.е. источник, описываемый геометрическим распределением. Если при этом целое положительное число m таково, что
то оптимальным посимвольным кодом для такого источника будет код, построенный в соответствии с предложенной С. Голомбом процедурой, согласно которой для любого кодируемого числа n при известном m кодовое слово образуют унарная запись числа
Чрезвычайно простая в реализации, но не всегда оптимальная разновидность кода Голомба в случае, когда m является степенью 2, называется кодом Райса. Просмотров: 3068
|
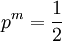 ,
,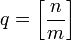 и кодированный в соответствии с описанной ниже процедурой остаток r от деления
и кодированный в соответствии с описанной ниже процедурой остаток r от деления 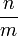 :
: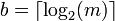 . Далее:
. Далее: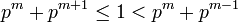 ,
,