Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Хеширование - Криптографические хеш-функции23 января 2011Оглавление: 1. Хеширование 2. Контрольные суммы 3. Криптографические хеш-функции 4. Применение хеш-функций Среди множества существующих хеш-функций принято выделять криптографически стойкие, применяемые в криптографии. Для того, чтобы хеш-функция H считалась криптографически стойкой, она должна удовлетворять трем основным требованиям, на которых основано большинство применений хеш-функций в криптографии:
Данные требования не являются независимыми:
Следует отметить, что не доказано существование необратимых хеш-функций, для которых вычисление какого-либо прообраза заданного значения хеш-функции теоретически невозможно. Обычно нахождение обратного значения является лишь вычислительно сложной задачей. Атака «дней рождения» позволяет находить коллизии для хеш-функции с длиной значений n битов в среднем за примерно 2 вычислений хеш-функции. Поэтому n-битная хеш-функция считается криптостойкой, если вычислительная сложность нахождения коллизий для неё близка к 2. Для криптографических хеш-функций также важно, чтобы при малейшем изменении аргумента значение функции сильно изменялось. В частности, значение хеша не должно давать утечки информации даже об отдельных битах аргумента. Это требование является залогом криптостойкости алгоритмов хеширования, хеширующих пользовательский пароль для получения ключа. Просмотров: 3892
|
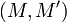 , имеющих одинаковый хеш.
, имеющих одинаковый хеш.