Интернет магазин китайских планшетных компьютеров |
||
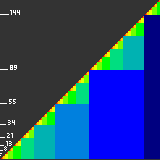
Компьютеры - Фибоначчиева система счисления22 января 2011Оглавление: 1. Фибоначчиева система счисления 2. Обобщение на вещественные числа 3. Фибоначчиево умножение Фибоначчиева система счисления — смешанная система счисления для целых чисел на основе чисел Фибоначчи F2=1, F3=2, F4=3, F5=5, F6=8 и т.д.
Представление натуральных чиселЛюбое неотрицательное целое число ОбоснованиеВ основе лежит теорема Цекендорфа — любое неотрицательное целое число представимо в виде суммы некоторого набора чисел Фибоначчи, не содержащего пары соседних чисел Фибоначчи. Причём представление такое единственно. Доказательство существования легко провести по индукции. Любое целое число ИспользованиеЮпана
Юпана
Предполагают, что некоторые разновидности юпаны использовали фибоначчиеву систему счисления, чтобы минимизировать необходимое для вычислений число зёрен. В теории информацииНа основе фибоначчиевой системы счисления строится код Фибоначчи — универсальный код для натуральных чисел, использующий последовательности битов. Поскольку комбинация 11 запрещена в Фибоначчиевой системе счисления, её можно использовать как маркер конца записи. Для составления кода Фибоначчи по записи числа в фибоначчиевой системе счисления следует переписать цифры в обратном порядке и приписать в конце ещё раз 1. То есть, кодовая последовательность имеет вид:
где n — номер самого старшего разряда с единицей. АрифметикаСложение чисел в позиционных системах счисления выполняется с использованием переноса, позволяющего устранять последствия переполнения разряда. Например, в двоичной системе: 01 + 01 = 02 = 10. В фибоначчиевой системе счисления дело обстоит сложнее:
Просмотров: 6007
|
||
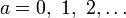 можно единственным образом представить через последовательность битов …εk…ε4ε3ε2:
можно единственным образом представить через последовательность битов …εk…ε4ε3ε2: 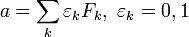 , причём последовательность {εk} содержит лишь конечное число единиц, и не имеет пар соседних единиц:
, причём последовательность {εk} содержит лишь конечное число единиц, и не имеет пар соседних единиц: 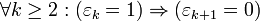 . За исключением последнего свойства, данное представление аналогично двоичной системе счисления.
. За исключением последнего свойства, данное представление аналогично двоичной системе счисления.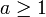 попадёт в промежуток между двумя соседними числами Фибоначчи, то есть для некоторого
попадёт в промежуток между двумя соседними числами Фибоначчи, то есть для некоторого 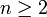 верно неравенство:
верно неравенство: 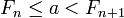 . Таким образом, a = Fn + a', где
. Таким образом, a = Fn + a', где 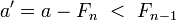 , так что разложение числа a' уже не будет содержать слагаемого Fn − 1.
, так что разложение числа a' уже не будет содержать слагаемого Fn − 1.