|
|
|
Компьютеры - Числа с плавающей запятой - Использование в вычислительных машинах23 января 2011
Оглавление:
1. Числа с плавающей запятой
2. Происхождение названия
3. Структура числа
4. Использование в вычислительных машинах
В вычислительных машинах показатель степени принято отделять от мантиссы буквой «E». Например, число 1,528535047×10 в большинстве языков программирования высокого уровня записывается как 1.528535047E-25.
Краткий обзор
Существует несколько способов того, как строки из цифр могут представлять числа:
- Наиболее распространённый путь представления значения числа из строки с цифрами — в виде целого числа — запятая по умолчанию находится в конце строки.
- В общем математическом представлении строка из цифр может быть сколь угодно длинной, а положение запятой обозначается путём явной записи символа запятой в нужном месте.
- В системах с представлением чисел в формате с фиксированной запятой существует определённое условие относительно положения запятой. Например, в строке из 8 цифр условие может предписывать положение запятой в середине записи. Таким образом, строка «00012345» обозначает число 1,2345.
- В экспоненциальной записи используют стандартный вид представления чисел. Число считается записанным в стандартном виде, если оно записано в виде aq, где a, называемое мантиссой, такое, что
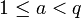 , n — целое, называется показатель степени и q — целое, основание системы счисления. То есть в мантиссе запятая помещается сразу после первой значащей цифры, считая слева направо, а дальнейшая запись даёт информацию о действительном значении числа. Например, период обращения спутника планеты Юпитера Ио, который равен 152853,5047 с, в стандартном виде можно записать как 1,528535047×10 с. Побочным эффектом ограничения на значения мантиссы является то, что в такой записи невозможно изобразить число 0. , n — целое, называется показатель степени и q — целое, основание системы счисления. То есть в мантиссе запятая помещается сразу после первой значащей цифры, считая слева направо, а дальнейшая запись даёт информацию о действительном значении числа. Например, период обращения спутника планеты Юпитера Ио, который равен 152853,5047 с, в стандартном виде можно записать как 1,528535047×10 с. Побочным эффектом ограничения на значения мантиссы является то, что в такой записи невозможно изобразить число 0.
- Запись в форме с плавающей запятой похожа на запись чисел в стандартном виде, но мантисса и экспонента записываются раздельно. Мантисса записывается в нормализованном формате — с фиксированной запятой, подразумеваемой после первой значащей цифры. Возвращаясь к примеру с Ио, запись в форме с плавающей запятой будет 1528535047 с показателем 5. Это означает, что записанное число в 10 раз больше числа 1,528535047, то есть для получения подразумеваемого числа запятая сдвигается на 5 разрядов вправо. Однако, запись в форме с плавающей запятой используется в основном в электронном представлении чисел, при котором используется основание системы счисления 2, а не 10. Кроме того, в двоичной записи мантисса обычно денормализована, то есть запятая подразумевается до первой цифры, а не после, и целой части вообще не имеется в виду — так появляется возможность и значение 0 сохранить естественным образом. Таким образом, десятичная 9 в двоичном представлении с плавающей запятой будет записана как мантисса +1001000…0 и показатель +0…0100. Отсюда, например, беды с двоичным представлением чисел типа одной десятой, для которой двоичное представление мантиссы оказывается периодической двоичной дробью — по аналогии с 1/3, которую нельзя конечным количеством цифр записать в десятичной системе счисления.
Запись числа в форме с плавающей запятой позволяет производить вычисления над широким диапазоном величин, сочетая фиксированное количество разрядов и точность. Например, в десятичной системе предоставления чисел с плавающей запятой операцию умножения, которую мы бы записали как
- 0,12 × 0,12 = 0,0144
в нормальной форме представляется в виде
- × =.
В формате с фиксированной запятой мы бы получили вынужденное округление
- 0,120 × 0,120 = 0,014.
Мы потеряли крайний правый разряд числа, так как данный формат не позволяет запятой «плавать» по записи числа.
Диапазон чисел, представимых в формате с плавающей запятой
Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. На обычной 32-битной вычислительной машине, использующей двойную точность, мантисса составляет 1 бит знак + 52 бита, показатель — 1 бит знак + 10 бит. Таким образом получаем диапазон точности примерно от 4,94×10 до 1.79×10. Пара значений показателя зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся значения NaN и +/-INF, получающихся в результате операций типа деления на ноль нуля, положительных и отрицательных чисел. Также сюда попадают денормализованные числа, у которых мантисса меньше единицы. В специализированных устройствах поддержка специальных чисел часто отсутствует. Существуют программные пакеты, в которых объём памяти выделенный под мантиссу и показатель задаётся программно, и ограничивается лишь объёмом доступной памяти ЭВМ.
| Точность |
Одинарная |
Двойная |
Расширенная |
| Размер |
4 |
8 |
10 |
| Число десятичных знаков |
7 |
15 |
19 |
| Наименьшее значение, denorm |
1,4×10 |
5,0×10 |
1,9×10 |
| Наименьшее значение, normal |
1,2×10 |
2,3×10 |
3,4×10 |
| Наибольшее значение |
3,4×10 |
1,7×10 |
1,1×10 |
| Поля |
S-E-F |
S-E-F |
S-E-I-F |
| Размеры полей |
1-8-23 |
1-11-52 |
1-15-1-63 |
- S — знак, E — показатель степени, I — целая часть, F — дробная часть
- Так же, как и для целых, знаковый бит — старший.
Машинная эпсилон
В отличие от чисел с фиксированной запятой, сетка чисел, которые способна отобразить арифметика с плавающей запятой, неравномерна: она более густая для чисел с малыми порядками и более редкая — для чисел с большими порядками. Но относительная погрешность записи чисел одинакова и для малых чисел, и для больших. Поэтому можно ввести понятие машинной эпсилон.
Машинной эпсилон называется наименьшее положительное число ε такое, что 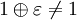 . Грубо говоря, числа a и b, соотносящиеся так, что . Грубо говоря, числа a и b, соотносящиеся так, что 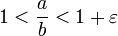 , машина не различает. , машина не различает.
Просмотров: 3793
|
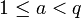 , n — целое, называется показатель степени и q — целое, основание системы счисления. То есть в мантиссе запятая помещается сразу после первой значащей цифры, считая слева направо, а дальнейшая запись даёт информацию о действительном значении числа. Например, период обращения спутника планеты Юпитера Ио, который равен 152853,5047 с, в стандартном виде можно записать как 1,528535047×10 с. Побочным эффектом ограничения на значения мантиссы является то, что в такой записи невозможно изобразить число 0.
, n — целое, называется показатель степени и q — целое, основание системы счисления. То есть в мантиссе запятая помещается сразу после первой значащей цифры, считая слева направо, а дальнейшая запись даёт информацию о действительном значении числа. Например, период обращения спутника планеты Юпитера Ио, который равен 152853,5047 с, в стандартном виде можно записать как 1,528535047×10 с. Побочным эффектом ограничения на значения мантиссы является то, что в такой записи невозможно изобразить число 0.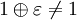 . Грубо говоря, числа a и b, соотносящиеся так, что
. Грубо говоря, числа a и b, соотносящиеся так, что 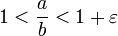 , машина не различает.
, машина не различает.