Интернет магазин китайских планшетных компьютеров |
|||
Компьютеры - Арифметико-логический способ представления троичных функций23 января 2011Оглавление: 1. Арифметико-логический способ представления троичных функций 2. Преобразование троичных функций 3. Функциональная полнота арифметико-логического способа представления троичных функций элементов 4. Представление основных троичных функций арифметико-логическим способом
это такой способ представления троичных функций, при котором любую трёхзначную функцию f можно представить в виде двух двухзначных 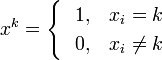 , где , где 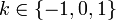 . .Простейший пример представления
Составим например аналитическую запись функции ~И-НЕ в соответствии с арифметико-логическим способом представления троичных функций. Таблица истинности функции ~И-НЕ определена в таблице 2. Функцию f1 можно представить в виде идеальной дизъюнктивной нормальной формы. Аргументами её являются характеристические функции, которые на наборах, где функция f принимает значение 1, равняется 1, то есть: f1=x1x2 V x1x2 V x1x2. Эту формулу можно получить непосредственно из таблицы истинности функции, если фиксировать внимание только на тех наборах переменных, для которых f=1, и заменив в них: xi=-1 переменной xi, x=0 переменной xi, xi=1 переменной xi. Полученные таким образом полные конъюнкции необходимо соединить знаком дизъюнкции. Функцию f2 можно также получить непосредственно из таблицы истинности функции, фиксируя внимание только на тех наборах переменных, для которых f(x1,x2=-1/ Таким образом, аналитически функцию ~И-НЕ можно представить в виде Просмотров: 4162
|
|||
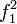 ,
, 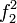 для значений которых выполняется арифметическая операция вычитания, то есть:
для значений которых выполняется арифметическая операция вычитания, то есть: 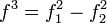 . Функция f задается трёхзначным алфавитом {1, − 1,0}. Функции
. Функция f задается трёхзначным алфавитом {1, − 1,0}. Функции