Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Алгоритм Полига Хеллмана - Исходные данные23 января 2011Оглавление: 1. Алгоритм Полига Хеллмана 2. Исходные данные 3. Сложность алгоритма Пусть задано сравнение
и известно разложение p − 1 на простые множители:
Необходимо найти натуральное число x, удовлетворяющее сравнению. Заметим, что на практике обычно рассматривается случай, когда a — первообразный корень по модулю p. В этом случае сравнение имеет решение при любом b, взаимно простом с p. Идея алгоритмаСуть алгоритма в том, что достаточно найти x по модулям
Данное сравнение решается за полиномиальное время в случае, если qi — небольшое, где c — некоторая константа). Описание алгоритма
Шаг 1. Составить таблицу значений {ri,j}, где
Просмотров: 4041
|
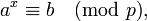
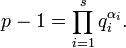
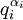 для всех i, а затем решение исходного сравнения можно найти с помощью китайской теоремы об остатках. Чтобы найти x по каждому из таких модулей, нужно решить сравнение:
для всех i, а затем решение исходного сравнения можно найти с помощью китайской теоремы об остатках. Чтобы найти x по каждому из таких модулей, нужно решить сравнение: 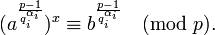
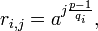
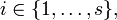
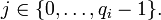 Шаг 2.
Для i от 1 до s:
Пусть
Шаг 2.
Для i от 1 до s:
Пусть
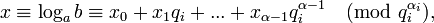 где
где
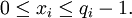 Тогда из следует, что
Тогда из следует, что
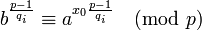 С помощью таблицы, составленной на шаге 1, находим x0.
Для j от 1 до α − 1
Рассматриваем сравнение
С помощью таблицы, составленной на шаге 1, находим x0.
Для j от 1 до α − 1
Рассматриваем сравнение
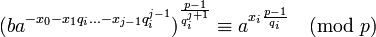 Решение опять же находится по таблице
Конец цикла по i
Конец цикла по j
Шаг 3. Найдя
Решение опять же находится по таблице
Конец цикла по i
Конец цикла по j
Шаг 3. Найдя 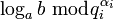 для всех i, находим
для всех i, находим 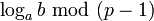 по китайской теореме об остатках.
по китайской теореме об остатках.