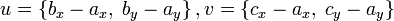Интернет магазин китайских планшетных компьютеров |
|
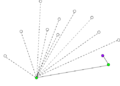
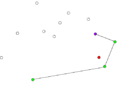
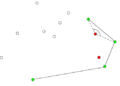
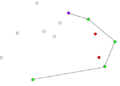
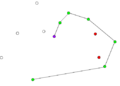
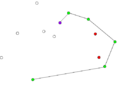
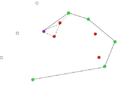
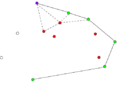
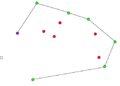
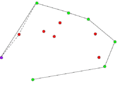
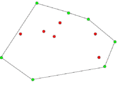
Компьютеры - Алгоритм Грэхема23 января 2011Оглавление: 1. Алгоритм Грэхема 2. Корректность сканирования по Грэхему алгоритм построения выпуклой оболочки в двухмерном пространстве. В этом алгоритме задача о выпуклой оболочке решается с помощью стека, сформированного из точек-кандидатов. Все точки входного множества заносятся в стек, а потом точки, не являющиеся вершинами выпуклой оболочки, со временем удаляются из него. По завершении работы алгоритма в стеке остаются только вершины оболочки в порядке их обхода против часовой стрелки. АлгоритмВ качестве входных данных процедуры Graham выступает множество точек Q, где Graham 1) Пусть p0 — точка из множества Q с минимальной координатой y или самая левая из таких точек при наличии совпадений 2) Пусть Для определения, образуют ли три точки a, b и c левый поворот, можно использовать обобщение векторного произведения на двумерное пространство, а именно условие левого поворота будет выглядеть следующим образом: uxvy − uyvx > 0, где
Просмотров: 2511
|
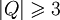 . В ней вызывается функция Top, которая возвращает точку, находящуюся на вершине стека S, не изменяя при этом его содержимое. Кроме того, используется также функция NextToTop, которая возвращает точку, расположенную в стеке S, на одну позицию ниже от верхней точки; стек S при этом не изменяется.
. В ней вызывается функция Top, которая возвращает точку, находящуюся на вершине стека S, не изменяя при этом его содержимое. Кроме того, используется также функция NextToTop, которая возвращает точку, расположенную в стеке S, на одну позицию ниже от верхней точки; стек S при этом не изменяется.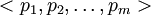 — остальные точки множества Q, отсортированные в порядке возрастания полярного угла,
измеряемого против часовой стрелки относительно точки p0
3) Push
4) Push
5) for i = 2 to m do
6) while угол, образованный точками NextToTop,Top и pi, образуют не левый поворот
7) do Pop
8) Push
9) return S
— остальные точки множества Q, отсортированные в порядке возрастания полярного угла,
измеряемого против часовой стрелки относительно точки p0
3) Push
4) Push
5) for i = 2 to m do
6) while угол, образованный точками NextToTop,Top и pi, образуют не левый поворот
7) do Pop
8) Push
9) return S