Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Алгоритм COS02 июня 2011Оглавление: 1. Алгоритм COS 2. Оценка сложности Алгоритм COS — субэкспоненциальный алгоритм дискретного логарифмирования в кольце вычетов по модулю простого числа. Был предложен в 1986 году. Исходные данныеПусть задано сравнение
Необходимо найти натуральное число x, удовлетворяющее сравнению. Описание алгоритма1 этап. Пусть
Сформируем множество
где q — простые.
. При этом так как J = O, то
причём это абсолютно наименьший вычет в этом классе и он имеет величину O. Поэтому вероятность его гладкости выше, чем для произвольных чисел, меньших p-1. Логарифмируя по основанию a, получим соотношение
Мы можем также считать, что a является гладким, то есть
откуда
4 этап. Для нахождения x введём новую границу гладкости L. Случайным перебором нахоим одно значение w, удовлетворяющее соотношению
u — простые числа «средней» величины. 5 этап. С помощью методов, анаогичных этапам 2 и 3, мы находим логарифмы простых чисел u, возникших на этапе 4. 6 этап. Находим ответ:
Просмотров: 1727
|
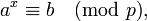
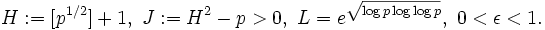
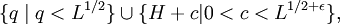
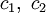 — такие, что 0 < ci < L, и
— такие, что 0 < ci < L, и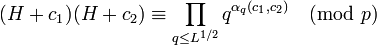
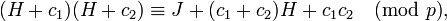
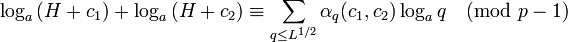
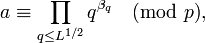
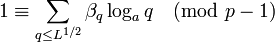
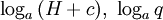 .
.